回溯
回溯法是递归的子集,通过将原问题分割成可迭代的子问题,将当前元素与更小的结果进行组合(就像回溯一样,回去和子结果组合)进行求解
例题
全排列
题目
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
|
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
|
示例 3:
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums 中的所有整数 互不相同
分析
全排列问题是回溯法的经典题型。[a, b, c, ...]的全排列tot(n)可以视作第一个元素和之后所有元素的全排列进行组合,第一个“主导”元素可以由所有元素轮流担任,因此将该问题分解为n * tot(n - 1),后者可以继续迭代分解(很像全排列公式);当数组中只有一个元素时,全排列就是自己,直接返回(基本情况)。
代码如下
class Solution {
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 1) {
List<List<Integer>> list = new ArrayList<>();
List<Integer> l = new ArrayList<>();
l.add(nums[0]);
list.add(l);
return list;
}
List<List<Integer>> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
swap(nums, 0, i);
int[] subArr = Arrays.copyOfRange(nums, 1, nums.length);
List<List<Integer>> tmpList = permute(subArr);
for (List<Integer> l : tmpList) {
l.add(0, nums[0]);
list.add(l);
}
swap(nums, 0, i);
}
return list;
}
void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
|
子集
题目
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的
子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
|
示例 2:
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums 中的所有元素 互不相同
分析
依然采用迭代分解(分治法)。[a, b, c, ...]的幂集P(n)可以看作首元素a与之后的子数组的幂集进行组合,可以加入a,也可以不加入a,即2 * P(n - 1)(正是幂集公式)。
代码如下
class Solution {
public List<List<Integer>> subsets(int[] nums) {
if (nums.length == 0) {
List<List<Integer>> list = new ArrayList<>();
List<Integer> l = new ArrayList<>();
list.add(l);
return list;
}
int[] subArr = Arrays.copyOfRange(nums, 1, nums.length);
List<List<Integer>> tmp = subsets(subArr);
List<List<Integer>> list = new ArrayList<>();
for (List<Integer> l : tmp) {
list.add(l);
}
for (List<Integer> l : tmp) {
l = new ArrayList<>(l);
l.add(0, nums[0]);
list.add(l);
}
return list;
}
}
|
电话号码的字母组合
题目
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
|
示例 2:
示例 3:
输入:digits = "2"
输出:["a","b","c"]
|
提示:
0 <= digits.length <= 4digits[i] 是范围 ['2', '9'] 的一个数字。
分析
敲数字d~1~d~2~d~3~…得到的字符串集合S(n)可以视作首数字d1对应的所有字母和去掉首数字后的数字串对应的字符串集合S(n - 1)的所有组合,因此得到递归求解的公式S(n) = [one of map(d1)] appends S(n - 1), 当数字串为空时,返回一个空集合(基础情况)。
代码如下
class Solution {
String[] alphabets = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public List<String> letterCombinations(String digits) {
if (digits.length() == 0) {
return new ArrayList<>();
}
List<String> list = new ArrayList<>();
List<String> tmp = letterCombinations(digits.substring(1));
if (tmp.isEmpty()) {
tmp.add("");
}
for (String s : tmp) {
for (char c : alphabets[digits.charAt(0) - '0'].toCharArray()) {
String t = s;
t = c + t;
list.add(t);
}
}
list.remove("");
return list;
}
}
|
组合总和
题目
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
|
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
|
示例 3:
输入: candidates = [2], target = 1
输出: []
|
提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates 的所有元素 互不相同1 <= target <= 40
分析
candidates是无重复的,这大大减轻了我们的工作量。对于一组可能的组合,比如2 + 2 + 3 = 7, 我们发现2 + 3 = 7 - 2, 3 = 7 - 2 - 2, 3就在candidates里(于是找到了一组)!而每次减的元素2也是数组中的元素!所以想到了一种回溯的方式:只要target仍然不小于2,我们就先判断target是否直接在candidates中存在,然后枚举candidates中的元素can[i],用同样的方式(递归调用)判断target - can[i]的情况,其结果(不为空)与can[i]的组合就是target情况时的结果;当上层判断完target - can[i]的情况时,需将can[i]从candidates中去除,防止计算重复情况。
几点优化:
- 可以先把
candidates排序方便后续处理
- 当
can[i] >= target时就可以退出了
代码如下
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
return combine(candidates, target);
}
List<List<Integer>> combine(int[] candidates, int target) {
if (target < 2) {
return new ArrayList<>();
}
List<List<Integer>> list = new ArrayList<>();
if (find(candidates, target)) {
List<Integer> l = new ArrayList<>();
l.add(target);
list.add(l);
}
while (candidates.length > 0) {
int cur = candidates[0];
if (cur >= target) {
break;
}
List<List<Integer>> tmpList = combine(candidates, target - cur);
if (!tmpList.isEmpty()) {
for (List<Integer> tmp : tmpList) {
tmp.add(0, cur);
list.add(tmp);
}
}
candidates = Arrays.copyOfRange(candidates, 1, candidates.length);
}
return list;
}
boolean find(int[] nums, int key) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] == key) {
return true;
} else if (nums[mid] > key) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return false;
}
}
|
括号生成
题目
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
|
示例 2:
提示:
分析
一般的分治思想无法解决本题,比如认为n的所有情况可以视作n - 1的所有情况中的每个字符串s与括号的任意组合s() / ()s / (s),但是这种方法无法生成(())(())。所以我们不能从括号对的角度出发(粒度太大),而应该从单括号的角度出发,每次只填入一个括号。具体来说,我们可以用一个参数记录当前字符串的填写进度,再记录当前还可以填入的左括号以及尚未被匹配的左括号(右括号不必记录,思考为什么);若当前还有(可以填入:则可以尝试填入一个(,若当前还有尚未被匹配的(,则也可以尝试填入);否则:只能填入)。当没有左括号可以填入且没有尚未被匹配的(时,当前记录的字符串就是一个结果且不会重复(思考为什么)。
右括号不必记录的原因:右括号不能先填入,只有存在未匹配的左括号时才可以填入右括号,只要左括号还能填,右括号就一定还有剩余,而两个参数记录了左括号的所有信息,所以右括号可以被左括号完全映射。
不会重复:从来没有回过头,当前位置填的不是(就是),当填了(时就一定和填了)的情况不同,不会出现重复。
代码如下
class Solution {
public List<String> generateParenthesis(int n) {
generate(n, 0, "");
return ans;
}
List<String> ans = new ArrayList<>();
void generate(int left, int nowLeft, String current) {
if (left == 0 && nowLeft == 0) {
ans.add(current);
return;
}
List<String> ans = new ArrayList<>();
if (left > 0) {
generate(left - 1, nowLeft + 1, current + "(");
if (nowLeft > 0) {
generate(left, nowLeft - 1, current + ")");
}
} else {
generate(0, nowLeft - 1, current + ")");
}
}
}
|
单词搜索
题目
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
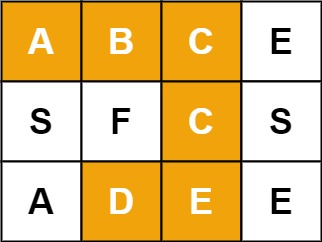
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
|
示例 2:
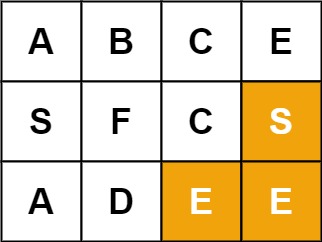
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
|
示例 3:

输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
|
提示:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board 和 word 仅由大小写英文字母组成
分析
回溯法的经典案例,采用DFS,先尝试往一个方向搜索到底。**字串"ABCCED"的匹配过程为:尝试站在A上,匹配"BCCED",尝试站在B上,匹配"CCED"…(不能走回头路)**每次匹配的过程都是一致的,因此可以递归调用,当某一次没有任何邻居能匹配上字串首字符时,匹配失败就会返回到上一个位置(发生回溯),以此类推。当字串为空时证明匹配成功。
注:匹配过程走不能回头路!
代码如下
class Solution {
public boolean exist(char[][] board, String word) {
char start = word.charAt(0);
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == start) {
if (search(board, i, j, word.substring(1))) {
return true;
}
}
}
}
return false;
}
boolean search(char[][] board, int i, int j, String target) {
if (target.length() == 0) {
return true;
}
char start = target.charAt(0);
board[i][j] ^= 0xFFFFFFFF;
if (i - 1 >= 0 && board[i - 1][j] == start && search(board, i - 1, j, target.substring(1))) {
return true;
} else if (i + 1 < board.length && board[i + 1][j] == start && search(board, i + 1, j, target.substring(1))) {
return true;
} else if (j + 1 < board[0].length && board[i][j + 1] == start && search(board, i, j + 1, target.substring(1))) {
return true;
} else {
boolean tmp = j - 1 >= 0 && board[i][j - 1] == start && search(board, i, j - 1, target.substring(1));
board[i][j] ^= 0xFFFFFFFF;
return tmp;
}
}
}
|
分割回文串
题目
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
|
示例 2:
提示:
1 <= s.length <= 16s 仅由小写英文字母组成
分析
TBD




