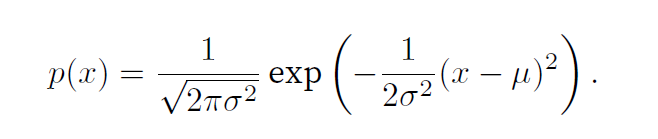线性神经网络

source code: NJU-ymhui/DeepLearning: Deep Learning with pytorch (github.com)

use git to clone: https://github.com/NJU-ymhui/DeepLearning.git

/Linear

vectorization_acceleration.py timer.py normal.py linear_regression_self.py linear_regression_lib.py image.py softmax_self.py

写在前面

参考书籍

Aston Zhang, Zachary C. Lipton, Mu Li, Alexander J. Smola. Dive into Deep Learning. 2020.

简介 - Dive-into-DL-PyTorch (tangshusen.me)

线性回归

线性模型

线性模型的基础是线性假设，即因变量=各自变量的加权和+偏移。

公式

ŷ = w~1~x~1~ + w~2~x~2~ + … + w~n~x~n~ + b => ŷ = w^T^x + b

其中向量x对应的是一个样本数据，如果将一个数据集的全部样本纳入计算，将有：

ŷ = Xw + b

给定训练数据特征X和对应的已知标签y，线性回归的目标是找到一组权重向量w和偏置b：当给定从X的同分布中取样的新样本特征时，这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。

噪声项

真实情况中，即便给定数据集预测结果的最佳模型是线性的，也一定会存在一些不可避免的观测误差，所以加入一个噪声项来考虑观测误差带来的影响。

即：ŷ = w^T^x + b + ϵ，ϵ为噪声项

损失函数

我们需要一个指标来度量我们**对于数据集拟合的好坏，**损失函数(loss function)应运而生。损失函数可以量化实际值与预测值之间的差距，通常选择非负值作为损失，损失越小预测越准，为0时为完美预测。

回归问题中常用的损失函数是平方误差函数

平方误差函数

ŷ为预测值，y为实际值

l(w, b) = 0.5 * (ŷ - y)^2^ // 对于单个样本

对于全体样本，我们还需要计算一个损失均值，即各样本损失求和的均值

在训练模型时，我们期望找到的一组参数(w, b)能够最小化损失均值（不针对某个样本，而是针对全体数据集）

解析解

由于线性回归是一个相对比较简单的优化问题，因此它的解(w, b)可以直接被公式表达，称之为解析解；遗憾的是，大部分其他模型并不具备解析解。

线性回归的解析解 w^*^

即最小化损失均值，也就是最小化总损失(y - ŷ)

其解析解w^^**为: **w^^ = (X^T^X)^-1^ X^T^y

随机梯度下降

这是一种优化算法，内容比较复杂，详见3.1 线性回归 - Dive-into-DL-PyTorch (tangshusen.me)

矢量化加速

对计算进行矢量化，可以利用线性代数库，而不用在Python中编写开销高昂的for循环。

首先定义一个计时器

code

import time
import numpy as np


class Timer:
    """记录多次运行时间"""


def __init__(self):
    self.times = []
    self.start()


def start(self):
    """启动计时器"""
    self.tik = time.time()


def stop(self):
    """停止计时器并将时间记录在列表中"""
    self.times.append(time.time() - self.tik)
    return self.times[-1]


def avg(self):
    """返回平均时间"""
    return sum(self.times) / len(self.times)


def sum(self):
    """返回时间总和"""
    return sum(self.times)


def cumsum(self):
    """返回累计时间"""
    return np.array(self.times).cumsum().tolist()

def compare_forloop_tensor():
    # 对比for循环和张量加
    a = torch.arange(100000)
    b = torch.arange(100000)
    res = torch.zeros(100000)
    clock = Timer()
    for i in range(len(a)):
        res[i] += a[i] + b[i]
    print(f'use for loop: {clock.stop(): .5f} sec')
    clock.start()
    c = a + b
    print(f'use tensor: {clock.stop(): .5f} sec')

output

use for loop:  1.15502 sec
use tensor:  0.00100 sec

正态分布与平方损失

正态分布与线性回归关系密切，其概率密度函数如下

code

def normal(x, mu, sigma):
    # 正态分布公式
    p = 1 / math.sqrt(2 * math.pi * sigma ** 2)
    return p * np.exp(-0.5 / sigma ** 2 * (x - mu) ** 2)


def gauss_distribution():
    x = torch.arange(-7, 7, 0.01)  # 从-7 到 7，步长为0.01
    mu_sigma = [(0, 1), (0, 2), (3, 1)]  # 三种均值和标准差组合
    d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in mu_sigma], figsize=(4.5, 2.5), xlabel='x', ylabel='p(x)')
    plt.show()

之所以说正态分布和线性回归关系紧密，是因为我们可以假设噪声服从正态分布，这样就能把均方误差损失函数用于线性回归

详细解释可见3.1. Linear Regression — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

从0实现线性回归

线性回归是一个单层神经网络

从此节开始，将不会再单独列出pytorch等的语法以及数学公式，具体代码和公式均会体现在code板块中，可以自行阅读查看。

实现步骤：

1. 生成数据集
2. 读取数据集
3. 初始化模型参数
4. 定义模型
5. 定义损失函数
6. 定义优化算法
7. 训练模型

code

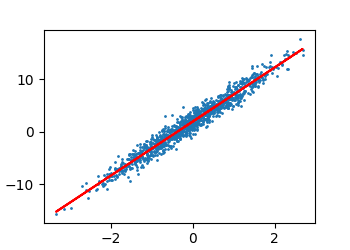
import random
import torch
from d2l import torch as d2l
from matplotlib import pyplot as plt
"""
从零开始实现一个线性回归模型
"""


def emit_data(w, b, num_examples):
    """
    create dataset with noise
    :w: params of weight
    :b: offset
    :num_examples: number of examples
    :return:
    """
    # according to y = Xw + b + epsilon, X is dataset, w is params, b is offset, epsilon is noise
    shape = (num_examples, len(w))  # shape of dataset, examples.number * w.length (Xw need X.col == w.row)
    X = torch.normal(0, 1, shape)  # dataset X from standard normal distribution
    y = torch.matmul(X, w) + b
    # add noise epsilon
    noise = torch.normal(0, 0.01, y.shape)
    y += noise  # add noise
    return X, y.reshape((-1, 1))


def data_iter(batch_size, x, y):
    """
    读取数据集，根据原数据集可以生成一些批量样本
    :param batch_size:批量样本的大小
    :param x:
    :param y:
    :return:
    """
    number_examples = len(x)  # x is dataset features, length is number of examples
    indices = list(range(number_examples))
    random.shuffle(indices)  # “洗牌”，对列表进行随机排序，使列表中的每个元素都有可能出现在任意位置
    for i in range(0, number_examples, batch_size):  # 以指定的批量大小为步长，遍历列表，每次生成一个批量样本
        batch_indices = torch.tensor(indices[i:min(i + batch_size, number_examples)])  # 剩下不足一个批量大小的数据生成到一起
        yield x[batch_indices], y[batch_indices]


def linear_model(X, w, b):
    """
    define a linear model
    :return:
    """
    return torch.matmul(X, w) + b


def squared_loss(y_hat, y):
    """
    定义均方损失函数
    :param y_hat: predict
    :param y: actual
    :return:
    """
    # 在此例中我们有两个权重（特征）
    # sum((y_pred - y_act) ^ 2) / 2
    return (y_hat - y) ** 2 * 0.5


def sgd(param, lr, batch_size):
    """
    定义优化算法：梯度下降
    :param param 模型参数列表
    :param lr 学习率，控制参数更新的幅度
    :param batch_size 批量大小，用于计算梯度平均值
    :return:
    """
    with torch.no_grad():  # 禁用自动梯度计算，因为参数更新不需要跟踪梯度
        for param_i in param:
            param_i.data -= lr * param_i.grad / batch_size  # param_i.grad 是当前参数的梯度，除以 batch_size 以得到平均梯度
            param_i.grad.zero_()  # 梯度清零，为下一次迭代计算新的梯度做准备


def func(k, b, x):
    return k * x + b


if __name__ == '__main__':
    # actual params and offset
    actual_w = torch.tensor([1.14, 5.14])
    actual_b = 1.91981
    data_size = 1145

    # emit data
    features, labels = emit_data(actual_w, actual_b, data_size)
    print("features:")
    print(features)
    print("labels:")
    print(labels)
    # data in vision
    d2l.set_figsize()  # 设置绘图的尺寸
    d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)  # 绘制散点图
    # features[:, 1]表示特征的第二列数据, labels表示标签；.detach().numpy()用于从张量中提取数值。
    plt.xlabel = "features"
    plt.ylabel = "labels"
    # plt.show()

    # read data
    batch_size = 10  # 批量大小为10
    print("a batch of data:")
    for X, y in data_iter(batch_size, features, labels):
        print(X)
        print(y)
        break  # 看一下就行了

    # init out model's param
    # 创建了一个名为w的张量，形状为(2, 1)，值从均值为0、标准差为0.01的正态分布中随机生成，且要求计算梯度。
    w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)  # 作为模型初始权重
    # 创建了一个名为b的张量，形状为(1,)，初始值为0，同样要求计算梯度。这些操作通常用于初始化神经网络的权重和偏置项。
    b = torch.zeros(1, requires_grad=True)  # 作为模型初始偏移
    # 初始化这些参数之后，我们需要不断更新它们，直到足够拟合数据

    # start training
    # 首先为模板赋上此例中的具体值
    lr = 0.03  # 学习率是一个超参数，暂时指定为0.03
    num_epochs = 3  # 训练轮数也是一个超参数
    net = linear_model  # 神经网络采用线性模型
    loss = squared_loss  # 损失函数采用均方损失函数
    for epoch in range(num_epochs):
        for X, y in data_iter(batch_size, features, labels):
            l = loss(net(X, w, b), y)  # 计算X和y的小批量损失
            l.sum().backward()  # 反向传播，计算梯度
            sgd([w, b], lr, batch_size)  # 更新参数
        with torch.no_grad():
            train_l = loss(net(features, w, b), labels)
            print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
    print("real:")
    print(actual_w)
    print(actual_b)
    print("predict:")
    print(w)
    print(b)
    # in vision, real scatter is blue, predict linear is red
    draw_x = features[:, 1]
    draw_y = func(w[1], b, draw_x)
    d2l.plt.plot(draw_x, draw_y.detach().numpy(), color="red")
    plt.show()

output

features:
tensor([[ 1.2594, -0.1781],
        [ 0.0551,  0.0021],
        [ 0.5613, -0.4662],
        ...,
        [-0.1275,  0.3930],
        [-0.5470,  0.7300],
        [-0.0886,  0.5512]])
labels:
tensor([[2.4401],
        [2.0031],
        [0.1762],
        ...,
        [3.7953],
        [5.0566],
        [4.6438]])
a batch of data:
tensor([[-0.4109,  0.5243],
        [-1.6386, -0.1570],
        [-0.8908,  0.8113],
        [-0.3493,  0.1824],
        [-0.1640, -0.5096],
        [ 0.1518, -1.7703],
        [-1.6326,  2.3128],
        [-0.2308, -1.2880],
        [-0.9320, -1.3867],
        [ 0.6465, -0.2461]])
tensor([[ 4.1418],
        [-0.7664],
        [ 5.0695],
        [ 2.4722],
        [-0.8736],
        [-7.0107],
        [11.9394],
        [-4.9565],
        [-6.2656],
        [ 1.4107]])
epoch 1, loss 0.018194
epoch 2, loss 0.000079
epoch 3, loss 0.000051
real:
tensor([1.1400, 5.1400])
1.91981
predict:
tensor([[1.1412],
        [5.1394]], requires_grad=True)
tensor([1.9196], requires_grad=True)

使用已有框架实现线性回归

现有的许多模型已经被研究很多了，许多现成的库可以直接调用; 由于数据迭代器、损失函数、优化器和神经网络层很常用，现代深度学习库也为我们实现了这些组件

code

import torch
import numpy as np
from torch.utils import data
from d2l import torch as d2l
from torch import nn  # 导入神经网络

"""
使用现有的库实现线性回归
"""


# 读取数据可以直接使用现有的data框架里的api
def load_data(data_tuple, batch_size, is_train=True):
    """实现一个pytorch迭代器"""
    # *用于解包，将data_tuple解包为多个参数，并作为独立的参数传入TensorDataset
    dataset = data.TensorDataset(*data_tuple)  # 将输入的元组数据转换为TensorDataset
    return data.DataLoader(dataset, batch_size, shuffle=is_train)  # 创建DataLoader，设置批量大小为batch_size


if __name__ == '__main__':
    # actual params and offset
    actual_w = torch.tensor([1.14, 5.14])
    actual_b = 1.91981
    data_size = 1145

    batch_size = 10
    features, labels = d2l.synthetic_data(actual_w, actual_b, data_size)  # 生成数据集也使用现成库
    data_iter = load_data((features, labels), batch_size)
    print(next(iter(data_iter)))  # 看一下效果，从可迭代对象data_iter中获取一个迭代器，并调用next()方法从该迭代器中取出下一个元素

    # 定义模型
    net = nn.Sequential(nn.Linear(2, 1))  # 选择现有库nn中的线性模型，输入维度为2，输出维度为1，即将两个输入特征映射成一个输出结果

    # init model
    net[0].weight.data.normal_(0, 0.01)  # 初始化权重参数, 均值为0，方差为0.01
    net[0].bias.data.fill_(0)  # 初始化偏置参数，0

    # 定义损失函数
    loss = nn.MSELoss()  # 均方误差损失函数

    # 定义优化算法
    opt = torch.optim.SGD(net.parameters(), lr=0.03)  # 随机梯度下降，学习率为0.03

    # train
    num_epochs = 3
    for epoch in range(num_epochs):
        l = 0.0
        for X, y in data_iter:
            l = loss(net(X), y)  # 计算损失
            opt.zero_grad()  # 梯度清零
            l.backward()  # 反向传播计算梯度
            opt.step()  # 更新参数
        print(f'epoch {epoch + 1}, loss {float(l):f}')
    print("real:")
    print(actual_w)
    print(actual_b)
    print("predict:")
    print(net[0].weight.data)
    print(net[0].bias.data)

output

[tensor([[-0.5939,  0.1061],
        [-0.1793, -0.2387],
        [ 0.1372, -0.0213],
        [ 0.0400,  1.5084],
        [ 0.7948, -0.4549],
        [ 1.9140, -0.7444],
        [-0.1117,  0.3958],
        [-2.2069, -1.2470],
        [-0.2498, -0.0193],
        [ 0.0258,  1.3288]]), tensor([[ 1.7824],
        [ 0.4828],
        [ 1.9654],
        [ 9.7057],
        [ 0.4970],
        [ 0.2660],
        [ 3.8387],
        [-7.0099],
        [ 1.5277],
        [ 8.7718]])]
epoch 1, loss 0.000083
epoch 2, loss 0.000095
epoch 3, loss 0.000060
real:
tensor([1.1400, 5.1400])
1.91981
predict:
tensor([[1.1394, 5.1387]])
tensor([1.9191])

softmax回归

softmax也是一个单层神经网络

分类问题

即取值是离散值的问题，比如是猫还是狗，成年还是未成年等。

softmax详细理论知识

详见3.4 softmax回归 - Dive-into-DL-PyTorch (tangshusen.me)

从零实现softmax回归

和从0实现线性回归同理，此处将从零实现softmax回归，使用接下来会介绍的Fashion-MNIST数据集

步骤如下：

1. 初始化模型参数
2. 定义softmax操作
3. 定义模型
4. 定义损失函数
5. 分类精度
6. 训练
7. 预测

code

TBD

使用已有框架实现softmax回归

TBD

图像分类数据集

MNIST数据集是图像分类中广泛使用的数据集之一，但作为基准数据集过于简单。此处将使用类似但更复杂的Fashion‐MNIST数据集

直接上代码

code

TBD