注意力机制

写在前面

参考书籍

Aston Zhang, Zachary C. Lipton, Mu Li, Alexander J. Smola. Dive into Deep Learning. 2020.

简介 - Dive-into-DL-PyTorch (tangshusen.me)

注意力机制

source code: NJU-ymhui/DeepLearning: Deep Learning with pytorch (github.com)

use git to clone: https://github.com/NJU-ymhui/DeepLearning.git

/attention

visualization.py batch_matrix.py nadaraya_watson.py score.py bahdanau.py multi_head.py self_attention.py position_encoding.py

注意力机制（Attention Mechanism）是一种在神经网络中用于提升模型性能和效率的重要技术，特别是在处理序列数据和复杂输入时。它通过让模型专注于输入的特定部分，从而提高对相关信息的利用。

其核心思想是：在处理数据时，模型不需要对所有输入数据赋予相等的关注，而是根据上下文动态调整关注的重点。

查询、键和值

查询：自主性提示

键：非自主性提示

值：感官输入

非自主性提示

指的是输入数据的特征，类似于感官输入，可以使用全连接层或汇聚层（如最大汇聚层或平均汇聚层）来处理。

自主性提示

在注意力机制中被称为查询（query），用于引导模型的注意力方向。

注意力机制的工作原理

• 给定一个查询（自主性提示），注意力机制通过计算查询与多个键（非自主性提示）的匹配程度，决定哪些值（感官输入）应该被关注。
• 每个值（感官输入）都有一个对应的键。模型根据查询和键的匹配情况，通过注意力汇聚来选择最相关的值。

即通过训练引导模型朝着指定方向搜索来加快效率，提升精确度

注意力的可视化

code

import torch
from d2l import torch as d2l


def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),
                  cmap='Reds'):
    """Show heatmaps of matrices."""
    # 使用SVG格式显示图像，以获得更清晰的视觉效果
    d2l.use_svg_display()

    # 提取矩阵的行数和列数，用于后续的图形网格布局
    num_rows, num_cols, _, _ = matrices.shape

    # 创建一个图形和子图网格，根据矩阵的行数和列数进行布局
    # figsize参数用于设置图形的大小，sharex和sharey参数确保子图之间共享x和y轴的刻度，squeeze=False以保持子图数组的维度
    fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,
                                 sharex=True, sharey=True, squeeze=False)

    # 遍历子图网格和矩阵，将矩阵可视化在相应的子图上
    for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):
        for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):
            # 在子图上绘制矩阵的图像
            pcm = ax.imshow(matrix.detach().numpy(), cmap=cmap)
            # 为最后一行的子图设置x轴标签
            if i == num_rows - 1:
                ax.set_xlabel(xlabel)
            # 为第一列的子图设置y轴标签
            if j == 0:
                ax.set_ylabel(ylabel)
            # 如果提供了标题，则为子图设置标题
            if titles:
                ax.set_title(titles[j])

    # 在图形的右侧添加一个颜色条，用于表示矩阵值的含义
    # shrink参数用于调整颜色条的大小
    fig.colorbar(pcm, ax=axes, shrink=0.6)
    d2l.plt.show()


if __name__ == '__main__':
    attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
    show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')

output

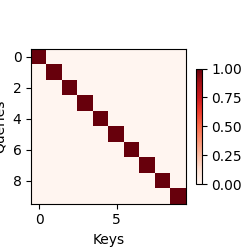
批量矩阵乘法

为了更有效地计算小批量数据的注意力，我们可以使用批量矩阵乘法

假设第一个小批量有n个矩阵，A1, A2, …, An，形状为a * b，第二个小批量也有n个矩阵B1, B2, …, Bn，形状为b * c，它们的批量矩阵乘法结果为A1B1, A2B2, …, AnBn，因此我们利用两个三维张量(A1, A2, …, An) (B1, B2, …, Bn)，形状分别为(n, a, b) (n, b, c)，批量矩阵乘法后的形状为(n, a, c)

torch.bmm(...)：批量矩阵乘法

code

import torch


if __name__ == '__main__':
    a = torch.ones((2, 1, 4))
    b = torch.ones((2, 4, 6))
    print(torch.bmm(a, b).shape)

    # 注意力背景下的批量矩阵乘法
    weights = torch.ones((2, 10)) * 0.1
    print("weights:")
    print(weights)
    print("after unsqueeze:")
    print(weights.unsqueeze(1))  # 通过添加维度从而可以利用批量矩阵乘法
    values = torch.arange(20, dtype=torch.float32).reshape((2, 10))
    print("values:")
    print(values)
    print("after unsqueeze:")
    print(values.unsqueeze(-1))  # 通过添加维度从而可以利用批量矩阵乘法
    print("calculate:")
    print(torch.bmm(weights.unsqueeze(1), values.unsqueeze(-1)))
    print(torch.mm(weights, values.T))

output

torch.Size([2, 1, 6])
weights:
tensor([[0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000,
         0.1000],
        [0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000,
         0.1000]])
after unsqueeze:
tensor([[[0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000,
          0.1000, 0.1000]],

        [[0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000,
          0.1000, 0.1000]]])
values:
tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.],
        [10., 11., 12., 13., 14., 15., 16., 17., 18., 19.]])
after unsqueeze:
tensor([[[ 0.],
         [ 1.],
         [ 2.],
         [ 3.],
         [ 4.],
         [ 5.],
         [ 6.],
         [ 7.],
         [ 8.],
         [ 9.]],

        [[10.],
         [11.],
         [12.],
         [13.],
         [14.],
         [15.],
         [16.],
         [17.],
         [18.],
         [19.]]])
calculate:
tensor([[[ 4.5000]],

        [[14.5000]]])
tensor([[ 4.5000, 14.5000],
        [ 4.5000, 14.5000]])

注意力汇聚

目前，我们已经知道，查询（自主性提示）和键（非自主性提示）之间的交互形成了注意力汇聚；而注意力汇聚有选择地聚合了值（感官输入）从而确定了最后的输出。本节将介绍注意力汇聚的一些细节，以便了解其工作方式。

Nadaraya-Watson核回归

Nadaraya-Watson核回归模型可用于演示带有注意力机制的机器学习。

我们用这样一个函数来模拟生成数据

其中噪声ϵ ~ N(0, 0.5^2)

code

import torch
from torch import nn
from d2l import torch as d2l
from visualization import show_heatmaps


def data_f(x):
    """生成训练数据"""
    return 2 * torch.sin(x) + x ** 0.8 + torch.normal(0, 0.5, x.shape)


def true_f(x):
    """生成真实数据"""
    return 2 * torch.sin(x) + x ** 0.8


if __name__ == '__main__':
    # 生成数据集
    n_train = 50
    x_train, _ = torch.sort(torch.rand(n_train) * 5)  # 为了之后更好地可视化，将训练数据集排序
    y_train = data_f(x_train)
    x_test = torch.arange(0, 5, 0.1)
    y_test = true_f(x_test)
    n_test = len(x_test)
    print(n_test)

    def plot_kernel_reg(y_hat):
        """绘制样本，不带噪声项的真实函数记为Truth，预测出的函数记为Pred"""
        d2l.plot(x_test, [y_test, y_hat], 'x', 'y', legend=['Truth', 'Pred'],
                 xlim=[0, 5], ylim=[-1, 5])
        d2l.plt.plot(x_train, y_train, 'o', alpha=0.5)
        d2l.plt.show()

    # 基于平均汇聚
    y_hat = torch.repeat_interleave(y_train.mean(), n_test)
    plot_kernel_reg(y_hat)

    # 基于非参数的注意力汇聚
    # 将x_test重复n_train次，然后重塑为矩阵，以准备进行注意力计算
    x_repeat = torch.repeat_interleave(x_test, n_train).reshape((-1, n_train))
    # 计算注意力权重，通过计算x_repeat和x_train之间的差异，应用softmax函数进行标准化
    attention_weights = nn.functional.softmax(-(x_repeat - x_train) ** 2 / 2, dim=1)
    # 通过加权训练数据的目标变量y_train来预测y_hat，权重为attention_weights
    y_hat = torch.matmul(attention_weights, y_train)
    plot_kernel_reg(y_hat)
    show_heatmaps(attention_weights.unsqueeze(0).unsqueeze(0),  # unsqueeze添加两个维度
                  xlabel='sorted training inputs',
                  ylabel='sorted testing inputs')

    # 基于带参数的注意力汇聚
    class NWKernelReg(nn.Module):
        def __init__(self, **kwargs):
            super().__init__(**kwargs)
            self.w = nn.Parameter(torch.rand((1, ), requires_grad=True))  # 初始化一个可训练参数w

        def forward(self, queries, keys, values):
            """
            前向传播方法，实现自注意力机制的计算。
            :param queries: 查询张量，模型的输入之一。
            :param keys: 键张量，用于计算注意力权重。
            :param values: 值张量，用于加权计算最终输出。
            :return: 经过注意力机制计算后的输出张量。
            """
            # 将查询张量(queries)重复展开，以匹配键张量(keys)的维度
            queries = torch.repeat_interleave(queries, keys.shape[1]).reshape((-1, keys.shape[1]))
            # 计算注意力权重
            # 通过softmax函数对计算出的权重进行归一化，使其和为1
            self.attention_weights = nn.functional.softmax(-((queries - keys) * self.w) ** 2 / 2, dim=1)
            # 应用注意力权重
            # 通过加权求和得到最终的输出
            return torch.bmm(self.attention_weights.unsqueeze(1), values.unsqueeze(-1)).reshape(-1)

    # 训练

    # 数据处理
    # 将训练集中的每个样本沿着第一维度重复n_train次，生成新的训练数据
    # 这样做的目的是为了在模型训练过程中增加样本多样性，增强模型的泛化能力
    x_tile = x_train.repeat((n_train, 1))
    # 同样的操作应用于标签数据，保证每个重复的样本仍然保留其正确的标签
    # 这是为了在增加样本多样性的同时，保持样本与其标签的一一对应关系
    y_tile = y_train.repeat((n_train, 1))
    # 通过屏蔽掉对角线元素，选择键值对
    keys = x_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
    values = y_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))

    # 模型选择，且在带参数的注意力汇聚中使用平方误差损失函数和随机梯度下降优化
    net = NWKernelReg()
    loss = nn.MSELoss(reduction='none')
    trainer = torch.optim.SGD(net.parameters(), lr=0.5)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])

    for epoch in range(5):
        # 将模型参数的梯度归零
        net.zero_grad()
        # 计算当前周期的损失
        l = loss(net(x_train, keys, values), y_train)
        # 反向传播损失
        l.sum().backward()
        # 更新模型参数
        trainer.step()
        # 可视化
        print(f'epoch %d, loss: %f' % (epoch + 1, l.sum()))
        animator.add(epoch + 1, float(l.sum()))
    # 查看损失迭代情况
    d2l.plt.show()

    # 测试
    keys = x_train.repeat((n_test, 1))  # 注意要用训练数据（带噪声的）去测试拟合，不然就完全一致了（因为带噪声的才是真实情况）
    values = y_train.repeat((n_test, 1))
    y_hat = net(x_test, keys, values).unsqueeze(1).detach()
    # 可视化
    plot_kernel_reg(y_hat)
    # 可视化注意力汇聚情况
    show_heatmaps(net.attention_weights.unsqueeze(0).unsqueeze(0),
                  xlabel='sorted training inputs',
                  ylabel='sorted testing inputs')

output

50

基于平均汇聚的拟合结果图

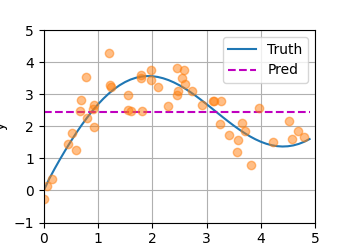
基于非参数的注意力汇聚的拟合结果图

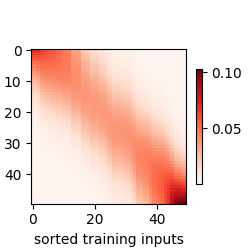
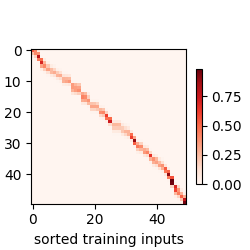
基于非参数的注意力可视化

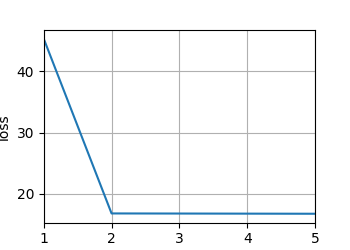
epoch 1, loss: 45.345715
epoch 2, loss: 16.821575
epoch 3, loss: 16.805058
epoch 4, loss: 16.788040
epoch 5, loss: 16.770472

损失值迭代结果图

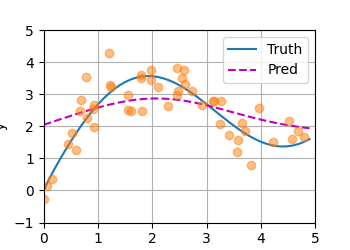
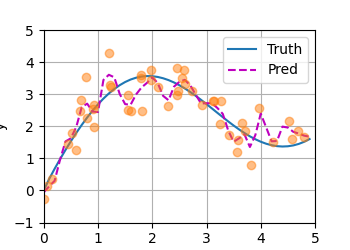
基于参数的注意力汇聚拟合结果图

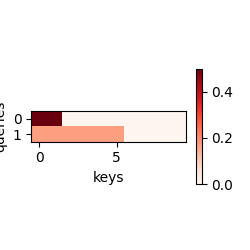
基于参数的注意力可视化

注意力评分函数

在之前的例子中，代入softmax函数中的公式（高斯核的指数部分）可以视作评分函数。

掩蔽softmax操作

在某些情况下，并非所有的值都应该被纳入注意力汇聚中，为了仅将有意义的词元作为值来获取注意力汇聚，可以指定一个有效序列长度（词元数量），以便过滤无意义值。

code

import torch
from torch import nn
from d2l import torch as d2l


def masked_softmax(X, valid_lens):
    """
    在最后一个轴上掩蔽元素来执行softmax操作
    :param X: 三维张量
    :param valid_lens: 一维或二维张量 
    :return: softmax操作后的结果
    """  # 最后一个维度代表特征数，因此在最后一个维度上操作即对每个特征都操作，且为了处理序列中不同元素的有效长度不同的情况
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:  # 1D张量，扩展为2D张量，重复元素即为复制这个向量
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])  # shape[1]为三维张量X第二个轴的元素个数
        else:
            valid_lens = valid_lens.reshape(-1)
        # 对序列进行掩码，将超过有效长度(valid_lens)的部分设置为极小值(value=-1e6), 以便后续处理中这些位置的影响会被忽略
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        # reshape保证形状不变，dim=-1在最后一个维度上计算softmax
        return nn.functional.softmax(X.reshape(shape), dim=-1)


if __name__ == '__main__':
    # 随机生成一个有两个矩阵的张量
    print(masked_softmax(torch.rand(2, 3, 4), torch.tensor([2, 3])))  # 第一个矩阵有效长度2，第二个矩阵有效长度3
    # 也可以为矩阵的每一行也指定长度
    print(masked_softmax(torch.rand((2, 3, 4)), torch.tensor([[1, 2, 1], [3, 4, 2]])))

output

tensor([[[0.4078, 0.5922, 0.0000, 0.0000],
         [0.5290, 0.4710, 0.0000, 0.0000],
         [0.5066, 0.4934, 0.0000, 0.0000]],

        [[0.3932, 0.3709, 0.2359, 0.0000],
         [0.4833, 0.2517, 0.2650, 0.0000],
         [0.2944, 0.2732, 0.4324, 0.0000]]])
tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
         [0.5413, 0.4587, 0.0000, 0.0000],
         [1.0000, 0.0000, 0.0000, 0.0000]],

        [[0.3292, 0.3518, 0.3190, 0.0000],
         [0.2038, 0.2110, 0.2027, 0.3825],
         [0.6417, 0.3583, 0.0000, 0.0000]]])

加性注意力

一般来说，当查询和键是不同长度的向量时，可以使用加性注意力作为评分函数。

一般做法：将查询和键连接起来后送入一个多层感知机，该感知机有一个隐藏层，隐藏层单元数是一个超参数，使用tanh作为激活函数。

code

import torch
from torch import nn
from d2l import torch as d2l


def masked_softmax(X, valid_lens):
    """
    在最后一个轴上掩蔽元素来执行softmax操作
    :param X: 三维张量
    :param valid_lens: 一维或二维张量 
    :return: softmax操作后的结果
    """  # 最后一个维度代表特征数，因此在最后一个维度上操作即对每个特征都操作，且为了处理序列中不同元素的有效长度不同的情况
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:  # 1D张量，扩展为2D张量，重复元素即为复制这个向量
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])  # shape[1]为三维张量X第二个轴的元素个数
        else:
            valid_lens = valid_lens.reshape(-1)
        # 对序列进行掩码，将超过有效长度(valid_lens)的部分设置为极小值(value=-1e6), 以便后续处理中这些位置的影响会被忽略
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        # reshape保证形状不变，dim=-1在最后一个维度上计算softmax
        return nn.functional.softmax(X.reshape(shape), dim=-1)


class AdditiveAttention(nn.Module):
    def __init__(self, queries_size, keys_size, num_hidden, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.w_q = nn.Linear(queries_size, num_hidden, bias=False)  # 用于key的输入层到隐藏层变换
        self.w_k = nn.Linear(keys_size, num_hidden, bias=False)  # 用于query的输入层到隐藏层变换
        self.w_v = nn.Linear(num_hidden, 1, bias=False)  # 隐藏层到输出层，即打分
        self.dropout = nn.Dropout(dropout)  # 传入暂退概率
        
    def forward(self, queries, keys, values, valid_lens):
        # 在多层感知机中对queries和keys作从输入层到隐藏层的变换
        queries = self.w_q(queries)
        keys = self.w_k(keys)
        # 假设queries: (batch_sz, n, d)->(batch_sz, n, 1, d); keys: (batch_sz, m, d)->(batch_sz, 1, m, d)
        # 广播机制求和后: (batch_sz, n, m, d)
        features = queries.unsqueeze(2) + keys.unsqueeze(1)  # queries在第二维加入新维度，keys在第一维加入新维度，可以利用广播机制相加
        features = torch.tanh(features)  # 激活
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # 初始输出的一个scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)


if __name__ == '__main__':
    # 准备数据
    # 初始化查询、键、值和有效长度
    # 查询: 使用正态分布生成的随机数组
    # 键: 一组全为1的数组
    # 值: 从0到39的连续数字的数组，每个数字重复两次
    queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
    # values的小批量，两个值矩阵是相同的
    values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)
    valid_lens = torch.tensor([2, 6])

    attention = AdditiveAttention(keys_size=2, queries_size=20, num_hidden=8, dropout=0.1)
    # 将模型设置为评估模式
    attention.eval()
    # 计算注意力权重
    # 注意：这里直接调用attention(queries, keys, values, valid_lens)，而不是使用.forward()方法
    # 因为在PyTorch中，如果模型没有处于训练模式，通常可以直接调用模型实例来进行预测或推理
    print(attention(queries, keys, values, valid_lens))  # 不要错用成attention.forward()
    # 可视化注意力
    d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)), xlabel='keys', ylabel='queries')
    d2l.plt.show()

output

tensor([[[ 2.0000,  3.0000,  4.0000,  5.0000]],

        [[10.0000, 11.0000, 12.0000, 13.0000]]], grad_fn=<BmmBackward0>)

缩放点积注意力

使用点积可以得到计算效率更高的评分函数，但是点积要求查询和键具有相同的长度。

缩放点积注意力的配分函数是

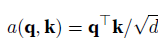
实践中，我们常通过小批量来提高计算效率，例如基于n个查询和m个键-值对计算注意力，其中查询和键的长度为d，值的长度为v，则查询Q、键K和值V的缩放点积注意力为

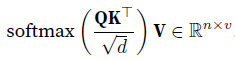
具体推导见11.3. Attention Scoring Functions — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

code

import math

import torch
from torch import nn
from d2l import torch as d2l


def masked_softmax(X, valid_lens):
    """
    在最后一个轴上掩蔽元素来执行softmax操作
    :param X: 三维张量
    :param valid_lens: 一维或二维张量 
    :return: softmax操作后的结果
    """  # 最后一个维度代表特征数，因此在最后一个维度上操作即对每个特征都操作，且为了处理序列中不同元素的有效长度不同的情况
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:  # 1D张量，扩展为2D张量，重复元素即为复制这个向量
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])  # shape[1]为三维张量X第二个轴的元素个数
        else:
            valid_lens = valid_lens.reshape(-1)
        # 对序列进行掩码，将超过有效长度(valid_lens)的部分设置为极小值(value=-1e6), 以便后续处理中这些位置的影响会被忽略
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        # reshape保证形状不变，dim=-1在最后一个维度上计算softmax
        return nn.functional.softmax(X.reshape(shape), dim=-1)


class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, queries_size, keys_size, num_hidden, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.w_q = nn.Linear(queries_size, num_hidden, bias=False)  # 用于key的输入层到隐藏层变换
        self.w_k = nn.Linear(keys_size, num_hidden, bias=False)  # 用于query的输入层到隐藏层变换
        self.w_v = nn.Linear(num_hidden, 1, bias=False)  # 隐藏层到输出层，即打分
        self.dropout = nn.Dropout(dropout)  # 传入暂退概率
        
    def forward(self, queries, keys, values, valid_lens):
        # 在多层感知机中对queries和keys作从输入层到隐藏层的变换
        queries = self.w_q(queries)
        keys = self.w_k(keys)
        # 假设queries: (batch_sz, n, d)->(batch_sz, n, 1, d); keys: (batch_sz, m, d)->(batch_sz, 1, m, d)
        # 广播机制求和后: (batch_sz, n, m, d)
        features = queries.unsqueeze(2) + keys.unsqueeze(1)  # queries在第二维加入新维度，keys在第一维加入新维度，可以利用广播机制相加
        features = torch.tanh(features)  # 激活
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # 初始输出的一个scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)


class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]  # d取queries最后一个维度的大小, 即查询和键的长度
        # 计算评分
        scores = torch.bmm(queries, keys.transpose(1, 2)) / math.sqrt(d)  # 套公式, 不过要注意keys的转置不能用.T，会报错(?)，要用transpose
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)


if __name__ == '__main__':
    # # 准备数据
    # # 初始化查询、键、值和有效长度
    # # 查询: 使用正态分布生成的随机数组
    # # 键: 一组全为1的数组
    # # 值: 从0到39的连续数字的数组，每个数字重复两次
    queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
    # values的小批量，两个值矩阵是相同的
    values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)
    valid_lens = torch.tensor([2, 6])

    # 缩放点积注意力

    queries = torch.normal(0, 1, (2, 1, 2))
    attention = DotProductAttention(dropout=0.5)
    attention.eval()  # 不进入训练模式，而是评估模式
    print(attention(queries, keys, values, valid_lens))
    d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)), xlabel='keys', ylabel='queries')
    d2l.plt.show()

output

tensor([[[ 2.0000,  3.0000,  4.0000,  5.0000]],

        [[10.0000, 11.0000, 12.0000, 13.0000]]])

Bahdanau注意力

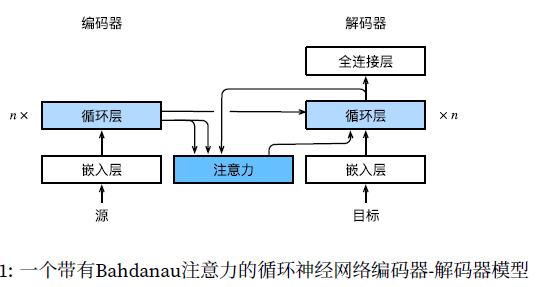
首先定义Bahdanau注意力，实现循环神经网络编码器-解码器；事实上，我们只需要重新定义解码器即可。

code

class AttentionDecoder(d2l.Decoder):
    """解码器接口"""
    def __init__(self, **kwargs):
        super(AttentionDecoder, self).__init__(**kwargs)

    def attention_weights(self):
        raise NotImplementedError

接下来，实现带有Bahdanau注意力的循环神经网络解码器

code

# TBD 先去看循环神经网络

多头注意力

模型原理及理论知识详见11.5. Multi-Head Attention — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

下面主要介绍实现

code

import torch
import math
from torch import nn
from d2l import torch as d2l


# 为了能使多个头并行计算，定义两个转置函数方便MultiHeadAttention类调用
# 具体来说，transpose_output反转了transpose_qkv的操作
def transpose_qkv(X, num_heads):
    """为了多头注意力的并行计算而改变形状"""
    # 输入X的形状:(batch_size，查询或者“键－值”对的个数，num_hiddens)
    # 输出X的形状:(batch_size，查询或者“键－值”对的个数，num_heads，
    # num_hidden / num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
    # 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数,
    # num_hidden / num_heads)
    X = X.permute(0, 2, 1, 3)
    # 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数,
    # num_hidden / num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])


def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)  # 为什么写成X.permute(0, 2, 1, 3).reshape(X.shape[0], X.shape[1], -1)不行


class MultiHeadAttention(nn.Module):
    def __init__(self, key_size, query_size, value_size, num_hidden, num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.attention = d2l.DotProductAttention(dropout=dropout)
        self.w_q = nn.Linear(query_size, num_hidden, bias=bias)
        self.w_k = nn.Linear(key_size, num_hidden, bias=bias)
        self.w_v = nn.Linear(value_size, num_hidden, bias=bias)
        self.w_o = nn.Linear(num_hidden, num_hidden, bias=bias)
        self.num_heads = num_heads

    def forward(self, queries, keys, values, valid_lens):
        # 使用不同的线性变换（w_q, w_k, w_v）处理查询、键和值之后，再根据多头注意力机制的需要，重新排列这些处理后的数据
        queries = transpose_qkv(self.w_q(queries), self.num_heads)
        keys = transpose_qkv(self.w_k(keys), self.num_heads)
        values = transpose_qkv(self.w_v(values), self.num_heads)
        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，以此类推
            valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim=0)

        # output的形状:(batch_size*num_heads, 查询的个数, num_hidden / num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # output_concat的形状: (batch_size, 查询的个数, num_hidden)
        output_concat = transpose_output(output, self.num_heads)
        return self.w_o(output_concat)


if __name__ == '__main__':
    # 测试MultiHeadAttention类
    num_hidden, num_heads = 100, 5
    attention = MultiHeadAttention(num_hidden, num_hidden, num_hidden, num_hidden, num_heads, dropout=0.5)
    print(attention.eval())
    batch_size, num_queries = 2, 4
    num_kvpairs, valid_lens = 6, torch.tensor([3, 2])
    X = torch.ones((batch_size, num_queries, num_hidden))
    Y = torch.ones((batch_size, num_kvpairs, num_hidden))
    print(attention(X, Y, Y, valid_lens).shape)

output

MultiHeadAttention(
  (attention): DotProductAttention(
    (dropout): Dropout(p=0.5, inplace=False)
  )
  (w_q): Linear(in_features=100, out_features=100, bias=False)
  (w_k): Linear(in_features=100, out_features=100, bias=False)
  (w_v): Linear(in_features=100, out_features=100, bias=False)
  (w_o): Linear(in_features=100, out_features=100, bias=False)
)
torch.Size([2, 4, 100])

自注意力和位置编码

自注意力

有了注意力机制之后，我们将词元序列输入注意力池中，以便同一组词元同时充当查询、键和值。具体来说，每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入，因此被称为自注意力。

code

import torch
from torch import nn
from d2l import torch as d2l


if __name__ == "__main__":
    # 初始化隐藏层神经元数量、头的数量
    num_hidden, num_heads = 100, 5
    attention = d2l.MultiHeadAttention(num_hidden, num_hidden, num_hidden, num_hidden, num_heads, dropout=0.5)
    print(attention.eval())  # 不训练

    # 初始化批量大小，查询的数量，有效词元长度
    batch_size, num_queries, valid_lens = 6, 6, torch.tensor([1, 1, 4, 5, 1, 4])
    X = torch.ones((batch_size, num_queries, num_hidden))  # 6个矩阵，每个矩阵都是6 * 100的
    tmp = attention(X, X, X, valid_lens)
    print(tmp)
    print(tmp.shape)

output

MultiHeadAttention(
  (attention): DotProductAttention(
    (dropout): Dropout(p=0.5, inplace=False)
  )
  (W_q): Linear(in_features=100, out_features=100, bias=False)
  (W_k): Linear(in_features=100, out_features=100, bias=False)
  (W_v): Linear(in_features=100, out_features=100, bias=False)
  (W_o): Linear(in_features=100, out_features=100, bias=False)
)
tensor([[[-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735]],

        [[-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735]],

        [[-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735]],

        [[-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735]],

        [[-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735]],

        [[-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735],
         [-0.1328,  0.1216, -0.0917,  ...,  0.0770, -0.4573, -0.2735]]],
       grad_fn=<UnsafeViewBackward0>)
torch.Size([6, 6, 100])

位置编码

自注意力为了并行计算放弃了顺序处理元素，为了使用序列的顺序信息，可以在输入表示中添加位置编码。

接下来介绍基于正弦函数和余弦函数的固定位置编码。

code

import torch
import math
from torch import nn
from d2l import torch as d2l


class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hidden, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P, 准备之后填充正弦值和余弦值
        self.P = torch.zeros((1, max_len, num_hidden))
        # 套公式
        X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / \
            torch.pow(10000, torch.arange(0, num_hidden, 2, dtype=torch.float32) / num_hidden)
        # 填充
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        """将输入张量X与位置编码矩阵相加，使模型能够感知序列中元素的位置信息"""
        # 相加时只取X也有的维度大小部分，因为self.P可能与X的维度不同，所以只取X维度相同的部分，即从0取到X.shape[1]
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        # .to(X.device)确保所有参与运算的张量都在同一个设备上，避免跨设备运算导致的错误或性能问题。
        return self.dropout(X)


if __name__ == '__main__':
    # 定义序列长度和编码维度
    num_steps, num_encoding = 60, 32
    # 初始化位置编码对象
    pos_encode = PositionalEncoding(num_encoding, 0)
    pos_encode.eval()
    # 处理一个全零张量
    X = pos_encode(torch.zeros((1, num_steps, num_encoding)))
    # 获取处理后的张量
    P = pos_encode.P[:, :X.shape[1], :]
    # 可视化
    d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
             figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
    d2l.plt.show()

output

绝对位置信息和相对位置信息

主要为理论介绍，详见11.6. Self-Attention and Positional Encoding — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

Transformer

TBD（等学完循环神经网络回来补~）