循环神经网络

写在前面

参考书籍

Aston Zhang, Zachary C. Lipton, Mu Li, Alexander J. Smola. Dive into Deep Learning. 2020.

简介 - Dive-into-DL-PyTorch (tangshusen.me)

循环神经网络前导

source code: NJU-ymhui/DeepLearning: Deep Learning with pytorch (github.com)

use git to clone: https://github.com/NJU-ymhui/DeepLearning.git

/RNN

markov.py text_preprocess.py nl_statistics.py random_sampling.py sequential_partition.py util.py rnn_self.py rnn_lib.py

到目前为止，我们一直都默认数据来自于某种分布，并且所有数据都是i.i.d（独立同分布）的，但是现实并非总是如此。比如一篇文章的文字是按某种顺序出现的，视频中的图像帧也按照特定顺序出现，网站的浏览行为也是有规律可循的…因此我们需要一个全新的模型来刻画这种现象。

本文介绍的循环神经网络可以很好地处理序列信息，通过引入状态变量存储过去的信息和当前的输入，可以给出当前的输出。

由于许多循环神经网络的例子都基于文本数据，因此本文着重介绍语言模型。

序列模型

处理序列数据需要统计工具和新的深度神经网络架构。

我们以股市交易数据为例入门，不妨用x~t~表示在t时间步(time step)时观测到的价格（注：t通常是离散的并在整数或其子集上变化）；如果希望在t日时较为准确地预测当日价格x~t~，应当有x~t~ ~ P(x~t~|x~t-1~…x~1~), 即在已知前t - 1日结果的前提下预测当日结果。

自回归模型

第一种策略，假设在现实情况下相当长的序列x~t−1~, . . . , x~1~可能是不必要的，因此我们只需要满足某个长度为τ的时间跨度，即使用观测序列x~t−1~, . . . , x~t−τ~ 。当下获得的最直接的好处就是参数的数量总是不变的，至少在t > τ时如此，这就使我们能够训练一个上面提及的深度网络。这种模型被称为自回归模型，因为它们是对自己执行回归。

第二种策略，如图8.1.2所示，是保留一些对过去观测的总结ht，并且同时更新预测ˆx~t~和总结ht。这就产生了基于ˆx~t~ = P(x~t~ | h~t~)估计x~t~，以及公式h~t~ = g(h~t−1~, x~t−1~)更新的模型。由于ht从未被观测到，这类模型也被称为隐变量自回归模型

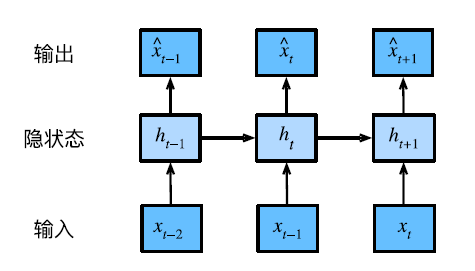
现在遇到一个新的问题，如何生成训练数据？一个常见的假设是，虽然特定值x~t~会改变，但序列本身的动力学不会改变，因为新的动力学一定受新数据的影响，而我们不可能用现有的数据预测出新的动力学。因此，整个序列的估计值都将通过以下的方式获得：

当处理对象离散时（比如单词）上述公式仍有效，只不过要用分类器而不是回归模型来估计P

马尔可夫模型Markov

理论部分

简单来说我们在上述公式的基础上，取τ = 1，得到一个一阶马尔可夫模型；再考虑*x~t~*仅是离散值，使用动态规划沿着马尔科夫链精确地计算结果。

详见9.1. Working with Sequences — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

训练

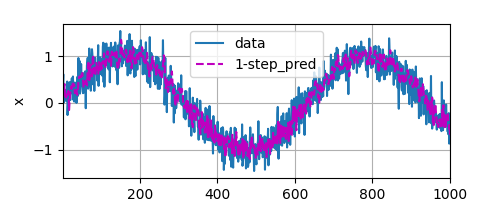
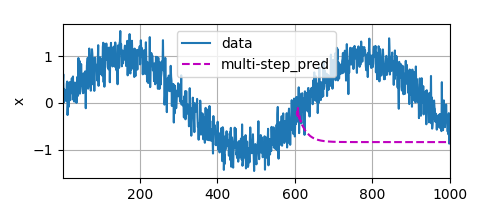
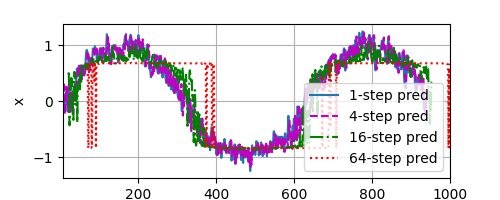
接下来我们使用正弦函数在背景噪声下生成一些序列数据。

然后基于这些数据做一些预测

code

import torch
from torch import nn
from d2l import torch as d2l


def generate_data(num):
    x = torch.arange(1, num + 1, dtype=torch.float32)
    y = torch.sin(0.01 * x) + torch.normal(0, 0.25, (num, ))
    return x, y


def init_weights(m):
    """初始化网络权重"""
    if type(m) == nn.Linear:
        nn.init.xavier_normal_(m.weight)


def get_net():
    """一个简单的多层感知机"""
    net = nn.Sequential(  # 一个有两个全连接层的多层感知机，使用ReLU激活函数
        nn.Linear(4, 10),
        nn.ReLU(),
        nn.Linear(10, 1)
    )
    net.apply(init_weights)
    return net


def train(net, train_iter, loss, epochs, lr):
    """训练模型，与前面格式一致，不再赘述"""
    trainer = torch.optim.Adam(net.parameters(), lr)  # Adam优化器
    for epoch in range(epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.sum().backward()
            trainer.step()
        print(f'epoch {epoch + 1}, '
              f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')


if __name__ == "__main__" :
    t = 1000
    time, x = generate_data(t)
    d2l.plot(time, [x], 'time', 'x', legend=['x'], xlim=[1, t], figsize=(5, 2))
    d2l.plt.show()
    # 接下来，我们将这个序列转换为模型的特征－标签（feature‐label）对; features-labels就是前面讲过的的自变量-因变量，还记得吗？
    # 基于嵌入维度τ，我们将数据映射为数据对yt = xt 和xt = [xt−τ , . . . , xt−1]。
    # 这比我们提供的数据样本少了τ个，因为我们没有足够的历史记录来
    # 描述前τ个数据样本。一个简单的解决办法是：如果拥有足够长的序列就丢弃这几项；另一个方法是用零填充序列
    # 使用前600个“特征－标签”对进行训练
    tau = 4  # 取tau = 4
    # 初始化特征矩阵，其中t是时间序列的长度，tau是时间步的大小
    features = torch.zeros((t - tau, tau))
    # 遍历时间步，构建特征矩阵
    for i in range(tau):
        features[:, i] = x[i:t - tau + i]  # 列是时间步，行是数据序列
    labels = x[tau:].reshape((-1, 1))
    batch_size, n_train = 16, 600  # 用前600个数据对来训练
    # 开始训练
    train_iter = d2l.load_array((features[:n_train], labels[:n_train]), batch_size, is_train=True)
    # 下面使用一个相当简单的架构训练模型：
    # 一个拥有两个全连接层的多层感知机，ReLU激活函数，平方损失函数
    loss = nn.MSELoss(reduction='none')
    net = get_net()
    epochs, lr = 5, 0.01
    train(net, train_iter, loss, epochs, lr)
    # 接下来开始预测
    onestep_pred = net(features)  # net(...)应用模型进行预测, 这里net(features)对其中的每个值依次作用产生输出，因此可以视作单步预测
    d2l.plot([time, time[tau:]], [x.detach().numpy(), onestep_pred.detach().numpy()],
             xlabel='time', ylabel='x', xlim=[1, t], legend=['data', '1-step_pred'], figsize=(5, 2))
    d2l.plt.show()

    # 以上均为单步预测，下面使用我们的预测(而不是原始数据)进行多步预测
    multistep_pred = torch.zeros(t)
    # 用我们的预测数据填充
    multistep_pred[:n_train + tau] = x[:n_train + tau]
    # 利用之前的预测值进行多步预测
    # f(xt) = f(xt-1, xt-2, ..., xt-tau)
    for i in range(n_train + tau, t):
        multistep_pred[i] = net(multistep_pred[i - tau:i].reshape((1, -1)))  # 这步预测结果出来后会被后面继续使用
    d2l.plot([time, time[n_train + tau:]], [x.detach().numpy(), multistep_pred[n_train + tau:].detach().numpy()],
             xlabel='time', ylabel='x', xlim=[1, t], legend=['data', 'multi-step_pred'], figsize=(5, 2))
    d2l.plt.show()
    # 可以看到超过某个值后预测的效果很差，几乎趋于一个常数，这是由于错误的累积

    # 基于k = 1, 4, 16, 64，通过对整个序列预测的计算，让我们更仔细地看一下k步预测的困难
    max_steps = 64
    features = torch.zeros((t - tau - max_steps + 1, tau + max_steps))
    # features的列i（i<tau）是来自x的观测，其时间步从（i）到（i+T-tau-max_steps+1）
    for i in range(tau):
        features[:, i] = x[i:i + t - tau - max_steps + 1]
    # 列i（i>=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
    for i in range(tau, tau + max_steps):
        features[:, i] = net(features[:, i - tau:i]).reshape(-1)

    # 可视化1, 4, 16, 64步预测的结果
    steps = (1, 4, 16, 64)
    d2l.plot([time[tau + i - 1: t - max_steps + i] for i in steps],
             [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
             legend=[f'{i}-step pred' for i in steps], xlim=[5, t],
             figsize=(5, 2))
    d2l.plt.show()

output

文本预处理

序列数据的另一种常见形式是文本；例如，一篇文章可以被看作单词甚至是字符序列。文本预处理通常采用以下步骤：

1. 将文本作为字符串加载到内存中。
2. 将字符串拆分为词元（如单词和字符）。
3. 建立一个词表，将拆分的词元映射到数字索引。(因为词元的类型是字符/字符串，而模型需要的是数字)
4. 将文本转换为数字索引序列，方便模型操作。

code

import torch
import collections
import re
from torch import nn
from d2l import torch as d2l


def read_time_machine():
    with open(d2l.download("time_machine"), 'r') as f:
        lines = f.readlines()
    return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]  # 只要英文字母且全小写


def tokenize(lines, token="word"):
    """
    将输入行拆分为词元
    :param lines: 输入的文本行列表
    :param token: 次元类型
    :return: 拆分后的列表
    """
    if token == 'word':
        return [line.split() for line in lines]
    elif token == 'char':
        return [list(line) for line in lines]
    else:
        raise ValueError("Invalid token flag: " + token)


# 建立一个词表，记录词元到数字的映射
class Vocab:
    def __init__(self, tokens=None, min_freq=0, reserved_tokens=None):
        if tokens is None:
            tokens = []
        if reserved_tokens is None:
            reserved_tokens = []
        # 按词元出现频率排序，降序
        counter = count_corpus(tokens)
        self._tokens_freq = sorted(counter.items(), key=lambda x: x[1], reverse=True)
        # 未知词元索引为0
        self.idx2token = ['<ink>'] + reserved_tokens  # 索引到词元
        self.token2idx = {token: idx for idx, token in enumerate(self.idx2token)}  # 词元到索引
        for token, freq in self._tokens_freq:
            if freq < min_freq:
                break
            if token not in self.token2idx:
                self.idx2token.append(token)
                self.token2idx[token] = len(self.idx2token) - 1

    def __len__(self):
        """返回词汇表中词汇的数量"""
        return len(self.idx2token)

    def __getitem__(self, tokens):
        """将一个或多个词汇转换为对应的索引，若词汇不存在，则返回未知词汇标识"""
        # 若tokens不是列表或元组，则直接返回该词汇的索引或未知词汇标识
        if not isinstance(tokens, (list, tuple)):
            return self.token2idx.get(tokens, self.unk)
        # 若tokens是列表或元组，则逐个转换为索引
        return [self.__getitem__(token) for token in tokens]

    def to_tokens(self, indices):
        """将一个或多个索引转换为对应的词汇"""
        # 若indices不是列表或元组，则直接返回该索引对应的词汇
        if not isinstance(indices, (list, tuple)):
            return self.idx2token[indices]
        # 若indices是列表或元组，则逐个转换为词汇
        return [self.idx2token[index] for index in indices]

    @property  # unk可以像属性一样被访问，而不需要调用方法
    def unk(self):
        return 0

    @property
    def token_freq(self):
        return self._tokens_freq


def count_corpus(tokens):
    """统计词元频率"""
    if len(tokens) == 0 or isinstance(tokens[0], list):
        tokens = [token for line in tokens for token in line]
    return collections.Counter(tokens)


def load_corpus_time_machine(max_tokens=-1):
    """整合所有功能，返回时光机器数据集的词元索引列表和词表"""
    lines = read_time_machine()
    tokens = tokenize(lines, token='char')  # 次元类型改为char
    vocab = Vocab(tokens)
    # 因为数据集中的每一个文本行不一定是一个句子或者段落
    # 所以展平到一个列表中
    corpus = [vocab[token] for line in tokens for token in line]
    if max_tokens > 0:
        # 如果限定了最大tokens的数量，我们就只取前max行
        corpus = corpus[:max_tokens]
    return corpus, vocab


if __name__ == '__main__':
    # 从时光机器文本中读取数据
    d2l.DATA_HUB['time_machine'] = (d2l.DATA_URL + 'timemachine.txt', '090b5e7e70c295757f55df93cb0a180b9691891a')
    lines = read_time_machine()
    print(len(lines))
    print(lines[0])
    print(lines[114])

    # 词元化
    tokens = tokenize(lines)
    for token in tokens[:10]:
        print(token)

    # 用上面拿到的数据集构建词表，看几个高频词及其索引
    vocab = Vocab(tokens)
    print("high frequency token and its index:")
    print(list(vocab.token2idx.items())[:10])

    # 现在就可以把每一行文本转化成索引序列了
    print("line text -> indices:")
    for i in [0, 10]:
        print(tokens[i], '->', vocab[tokens[i]])

    # 验证整合的功能
    print("check all functions in one:")
    tokens, vocab = load_corpus_time_machine()  # 接受词元索引列表和词表
    print((len(tokens), len(vocab)))

output

3221
the time machine by h g wells
but said the medical man staring hard at a coal in the fire if
['the', 'time', 'machine', 'by', 'h', 'g', 'wells']
[]
[]
[]
[]
['i']
[]
[]
['the', 'time', 'traveller', 'for', 'so', 'it', 'will', 'be', 'convenient', 'to', 'speak', 'of', 'him']
['was', 'expounding', 'a', 'recondite', 'matter', 'to', 'us', 'his', 'grey', 'eyes', 'shone', 'and']
high frequency token and its index:
[('<ink>', 0), ('the', 1), ('i', 2), ('and', 3), ('of', 4), ('a', 5), ('to', 6), ('was', 7), ('in', 8), ('that', 9)]
line text -> indices:
['the', 'time', 'machine', 'by', 'h', 'g', 'wells'] -> [1, 19, 50, 40, 2183, 2184, 400]
['twinkled', 'and', 'his', 'usually', 'pale', 'face', 'was', 'flushed', 'and', 'animated', 'the'] -> [2186, 3, 25, 1044, 362, 113, 7, 1421, 3, 1045, 1]
check all functions in one:
(170580, 28)

语言模型和数据集

模型原理部分参考9.3. Language Models — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

自然语言统计

code

import torch
from torch import nn
from d2l import torch as d2l


if __name__ == "__main__":
    lines = d2l.read_time_machine()
    tokens = d2l.tokenize(lines)
    corpus = [token for line in tokens for token in line]
    vocab = d2l.Vocab(corpus)
    print(vocab.token_freqs[:10])
    frequencies = [freq for token, freq in vocab.token_freqs]
    d2l.plot(frequencies, xlabel='token: x', ylabel='n(x)', xscale='log', yscale='log')
    d2l.plt.show()

    # 查看一下二元语法出现的概率
    bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
    bigram_vocab = d2l.Vocab(bigram_tokens)
    print(bigram_vocab.token_freqs[:10])

    # 再来看一下三元组
    trigram_tokens = [triple for triple in zip(corpus[:-2], corpus[1:-1], corpus[2:])]
    trigram_vocab = d2l.Vocab(trigram_tokens)
    print(trigram_vocab.token_freqs[:10])

    # 对比一下三种组合的出现概率图
    bigram_freq = [freq for token, freq in bigram_vocab.token_freqs]
    trigram_freq = [freq for token, freq in trigram_vocab.token_freqs]
    d2l.plot([frequencies, bigram_freq, trigram_freq], xlabel='token: x', ylabel='n(x)', xscale='log', yscale='log',
             legend=['single', 'double', 'triple'])
    d2l.plt.show()

output

[('the', 2261), ('i', 1267), ('and', 1245), ('of', 1155), ('a', 816), ('to', 695), ('was', 552), ('in', 541), ('that', 443), ('my', 440)]
[(('of', 'the'), 309), (('in', 'the'), 169), (('i', 'had'), 130), (('i', 'was'), 112), (('and', 'the'), 109), (('the', 'time'), 102), (('it', 'was'), 99), (('to', 'the'), 85), (('as', 'i'), 78), (('of', 'a'), 73)]
[(('the', 'time', 'traveller'), 59), (('the', 'time', 'machine'), 30), (('the', 'medical', 'man'), 24), (('it', 'seemed', 'to'), 16), (('it', 'was', 'a'), 15), (('here', 'and', 'there'), 15), (('seemed', 'to', 'me'), 14), (('i', 'did', 'not'), 14), (('i', 'saw', 'the'), 13), (('i', 'began', 'to'), 13)]

读取长序列数据

因为序列数据本质上是连续的，因此我们在处理数据时需要解决读取长序列数据的问题。

一种处理办法是：当序列过长而不能被模型一次性处理时，拆分这样的序列方便模型读取。假设我们将使用神经网络来训练语言模型，模型中的网络一次处
理具有预定义长度（例如n个时间步）的一个小批量序列。现在的问题是如何随机生成一个小批量数据的特征和标签以供读取。

首先，由于文本序列可以是任意长的，例如整本《时光机器》，于是任意长的序列可以被我们划分为具有相同时间步数的子序列。当训练我们的神经网络时，这样的小批量子序列将被输入到模型中。假设网络一次只处理具有n个时间步的子序列。

上图画出了从原始文本序列获得子序列的所有不同的方式，其中n = 5，并且每个时间步的词元对应于一个字符。

那么，我们应该选择哪一个呢？如果我们只选择一个偏移量，那么用于训练网络的、所有可能的子序列的覆盖范围将是有限的；因此，我们可以从随机偏移量开始划分序列，以同时获得覆盖性（coverage）和随机性（randomness）。下面介绍两个策略：随机采样，顺序分区

随机采样

在此策略下，每个样本都是在原始的长序列上任意捕获的子序列。在迭代过程中，来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻。对于语言建模，目标是基于到目前为止我们看到的词元来预测下一个词元，因此标签是移位了一个词元的原始序列。

code

import torch
from torch import nn
from d2l import torch as d2l
import random


def seq_fata_iter_random(corpus, batch_size, num_steps):
    """
    :param corpus:
    :param batch_size: 每个小批量中子序列样本的数量
    :param num_steps: 每个子序列中预定义的时间步数
    :return:
    """
    # 从语料库中随机选择一个片段作为开始, 切片内容包括num_steps - 1
    corpus = corpus[random.randint(0, num_steps - 1):]
    # 计算基于当前语料库长度和序列长度能够生成的序列数量
    # 减去1，是因为我们需要考虑标签
    num_sequences = (len(corpus) - 1) // num_steps
    # 创建一个列表，包含所有序列的起始索引，即长度为num_steps的子序列的起始索引
    initial_indices = list(range(0, num_sequences * num_steps, num_steps))
    # 在随机抽样的迭代过程中，
    # 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
    random.shuffle(initial_indices)

    # 定义一个辅助函数，根据给定的起始位置从语料库中提取序列
    def data(pos):
        # 返回从pos位置开始的长度为num_steps的序列
        return corpus[pos: pos + num_steps]

    num_batches = num_sequences // batch_size
    for i in range(0, num_batches * batch_size, batch_size):
        # initial_indices包含子序列的随机起始索引
        initial_indices_per_batch = initial_indices[i: i + batch_size]  # 从打乱顺序的起始索引列表中获取当前批次的起始索引
        # 根据当前批次中每个序列的起始索引，创建X（输入序列）和Y（目标序列）
        X = [data(j) for j in initial_indices_per_batch]
        Y = [data(j + 1) for j in initial_indices_per_batch]
        # 生成并提供输入和目标序列的张量表示
        yield torch.tensor(X), torch.tensor(Y)


if __name__ == '__main__':
    # 生成一个0 ~ 34的序列，并设置批量大小 = 2，时间步数 = 5
    # 这样可以生成(35 - 1) // 5 = 6个特征-标签子序列对
    seq = list(range(35))
    i = 1
    print("每个小批量中有两个子序列对:")
    for X, Y in seq_fata_iter_random(seq, batch_size=2, num_steps=5):
        print(f"第%d个\"特征-标签\"子序列对小批量" % i)
        print(f'X: {X}, \nY: {Y}')
        i += 1

output

每个小批量中有两个子序列对:
第1个"特征-标签"子序列对小批量
X: tensor([[0, 1, 2, 3, 4],
        [5, 6, 7, 8, 9]]), 
Y: tensor([[ 1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10]])
第2个"特征-标签"子序列对小批量
X: tensor([[20, 21, 22, 23, 24],
        [10, 11, 12, 13, 14]]), 
Y: tensor([[21, 22, 23, 24, 25],
        [11, 12, 13, 14, 15]])
第3个"特征-标签"子序列对小批量
X: tensor([[15, 16, 17, 18, 19],
        [25, 26, 27, 28, 29]]), 
Y: tensor([[16, 17, 18, 19, 20],
        [26, 27, 28, 29, 30]])

顺序分区

在迭代过程中，除了对原始序列可以随机抽样外，我们还可以保证两个相邻的小批量中的子序列在原始序列上也是相邻的。这种策略在基于小批量的迭代过程中保留了拆分的子序列的顺序，因此称为顺序分区。

code

import torch
import random


def seq_data_iter_sequential(corpus, batch_size, num_steps):
    """顺序分区策略生成小批量子序列"""
    # 从随机偏移量开始划分序列
    # 生成一个随机偏移量，用于乱序数据
    offset = random.randint(0, num_steps)
    # 计算基于批次大小可处理的令牌数量
    num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
    # 从乱序后的数据中创建输入序列Xs
    Xs = torch.tensor(corpus[offset: offset + num_tokens])
    # 从乱序后的数据中创建目标序列Ys，相比Xs向后移动了一个位置
    Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
    # 将序列Xs和Ys重塑为批次大小，以便于训练
    Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
    # 计算批次的数量
    num_batches = Xs.shape[1] // num_steps
    # 遍历所有序列，生成批次数据
    for i in range(0, num_steps * num_batches, num_steps):
        # X是当前批次的输入序列，长度为num_steps
        X = Xs[:, i: i + num_steps]
        # Y是当前批次的目标序列，长度为num_steps
        Y = Ys[:, i: i + num_steps]
        # 产出当前批次的输入序列X和目标序列Y
        yield X, Y


if __name__ == "__main__":
    # 数据配置与随机采样策略一致
    seq = list(range(35))
    for X, Y in seq_data_iter_sequential(seq, batch_size=2, num_steps=5):
        print(f'X: {X},\nY: {Y}')

output

X: tensor([[ 2,  3,  4,  5,  6],
        [18, 19, 20, 21, 22]]),
Y: tensor([[ 3,  4,  5,  6,  7],
        [19, 20, 21, 22, 23]])
X: tensor([[ 7,  8,  9, 10, 11],
        [23, 24, 25, 26, 27]]),
Y: tensor([[ 8,  9, 10, 11, 12],
        [24, 25, 26, 27, 28]])
X: tensor([[12, 13, 14, 15, 16],
        [28, 29, 30, 31, 32]]),
Y: tensor([[13, 14, 15, 16, 17],
        [29, 30, 31, 32, 33]])

将两种策略整合出辅助类

util.py

from d2l import torch as d2l


class SeqDataLoader:
    """加载序列数据的迭代器"""
    def __init__(self, batch_size, num_steps, use_random, max_tokens):
        if use_random:
            self.data_iter_fn = d2l.seq_data_iter_random
        else:
            self.data_iter_fn = d2l.seq_data_iter_sequential
        self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
        self.batch_size, self.num_steps = batch_size, num_steps

    def __iter__(self):
        return self.data_iter_fn(self.corpus, batch_size=self.batch_size, num_steps=self.num_steps)


def load_data_time_machine(batch_size, num_steps, use_random=False, max_tokens = 1e5):
    data_iter = SeqDataLoader(batch_size, num_steps, use_random, max_tokens)
    return data_iter, data_iter.vocab

循环神经网络

下面我们开始正式介绍循环神经网络！

理论部分详见9.4. Recurrent Neural Networks — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

无隐状态的神经网络：比如一个有单隐藏层的多层感知机

有隐状态的循环神经网络：…

基于循环神经网络的字符级语言模型、困惑度

详见9.4. Recurrent Neural Networks — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

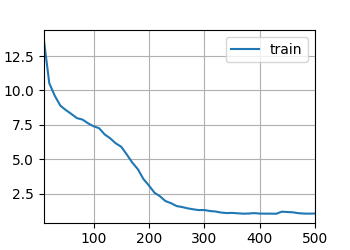
从零实现循环神经网络

此处将从头开始基于循环神经网络实现字符级语言模型，在时光机器数据集上训练。

code

import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


def get_params(vocab_size, num_hidden, device):
    """
    初始化神经网络的模型参数
    :param vocab_size 语言模型的输入输出来自同一个词表，因此他们具有相同的维度即词表大小
    :param num_hidden 隐藏层单元数，可调的超参数
    :param device
    """
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01

    # 隐藏层参数
    W_xh = normal((num_inputs, num_hidden))
    W_hh = normal((num_hidden, num_hidden))
    b_h = torch.zeros(num_hidden, device=device)
    # 输出层参数
    W_hq = normal((num_hidden, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params


def init_rnn_state(batch_size, num_hidden, device):
    """初始化时返回隐状态，返回值全0填充"""
    return torch.zeros((batch_size, num_hidden), device=device),


# rnn函数定义了如何在一个时间步内计算隐状态和输出
def rnn(inputs, state, params):
    # inputs形状: (时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状: (批量大小，词表大小)
    for X in inputs:
        # 使用tanh激活函数
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H, )


# 封装上述函数
class RNNModelScratch:
    """从零实现循环神经网络"""
    def __init__(self, vocab_size, num_hidden, device, get_params, init_state, forward_fn):
        self.vocab_size, self.num_hidden = vocab_size, num_hidden
        self.params = get_params(vocab_size, num_hidden, device)
        self.init_state, self.forward_fn = init_state, forward_fn

    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_fn(X, state, self.params)

    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hidden, device)


def predict_ch8(prefix, num_pred, net, vocab, device):
    """预测字符串prefix后面的内容"""
    state = net.begin_state(batch_size=1, device=device)
    outputs = [vocab[prefix[0]]]
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
    # 预热期
    for y in prefix[1:]:
        _, state = net(get_input(), state)
        outputs.append(vocab[y])
    # 预测num_pred步
    for _ in range(num_pred):
        y, state = net(get_input(), state)
        outputs.append(int(y.argmax(dim=1).reshape(1)))  # 把向量转化为索引
    return ''.join([vocab.idx_to_token[i] for i in outputs])  # 索引转化为token


def grad_clipping(net, theta):
    """裁剪梯度"""
    if isinstance(net, nn.Module):
        params = [p for p in net.parameters() if p.requires_grad]
    else:
        params = net.params
    norm = torch.sqrt(sum(torch.sum(p.grad ** 2) for p in params))
    if norm > theta:
        for param in params:
            param.grad[:] *= theta / norm


# 训练
def train_epoch_ch8(net, train_iter, loss, updator, device, use_random_iter):
    """训练网络一个迭代周期"""
    state, timer = None, d2l.Timer()
    metric = d2l.Accumulator(2)  # 训练损失之和
    for X, Y in train_iter:
        if state is None or use_random_iter:
            # 如果state还没有初始化或者使用随机采样
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            if isinstance(net, nn.Module) and not isinstance(state, tuple):
                state.detach_()
            else:
                for s in state:
                    s.detach_()
        y = Y.T.reshape(-1)
        X, y = X.to(device), y.to(device)
        y_hat, state = net(X, state)
        l = loss(y_hat, y.long()).mean()
        if isinstance(updator, torch.optim.Optimizer):
            updator.zero_grad()
            l.backward()
            grad_clipping(net, 1)
            updator.step()
        else:
            l.backward()
            grad_clipping(net, 1)
            # 因为已经调用过mean方法
            updator(batch_size=1)
        metric.add(y.numel() * l, y.numel())
    # 第一个返回值是困惑度perplexity，用于衡量语言模型的性能
    return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()


# 循环神经网络模型的训练函数
def train_ch8(net, train_iter, vocab, lr, num_epochs, device, use_random=False):
    """训练模型"""
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', ylabel='perplexity', legend=['train'], xlim=[10, num_epochs])
    # 初始化
    if isinstance(net, nn.Module):
        updator = torch.optim.SGD(net.parameters(), lr)
    else:
        updator = lambda batch_size: d2l.sgd(net.params, lr, batch_size)  # 接受一个参数批量大小
    # 预测函数
    predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)  # 接受一个参数初始序列
    # 训练和预测
    perplexity, speed = -1, -1
    for epoch in range(num_epochs):
        perplexity, speed = train_epoch_ch8(net, train_iter, loss, updator, device, use_random)
        # print(f'perplexity:  {perplexity}')
        if (epoch + 1) % 10 == 0:
            animator.add(epoch + 1, (perplexity,))
    d2l.plt.show()  # 可视化困惑度动态迭代结果
    print(f'perplexity:  {perplexity}, {speed} tokens / per second, on {device}')
    print("predict 'time traveller':")
    print(predict("time traveller"))
    print(predict("traveller"))


if __name__ == "__main__":
    batch_size, num_steps = 32, 35
    train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

    # 之前一直将词元表示为一个索引, 但这样会使得模型难以学习(一个标量), 因此引入独热编码将词元映射为向量(互不相同的索引映射为互不相同的单位向量)
    print(F.one_hot(torch.tensor([0, 2, 3]), len(vocab)))
    # 每次采样的小批量数据形状是二维张量：（批量大小，时间步数）
    # one_hot函数将这样一个小批量数据转换成三维张量，张量的最后一个维度等于词表大小
    # 转换输入的维度，以便获得形状为（时间步数，批量大小，词表大小）的输出
    X = torch.arange(10).reshape((2, 5))
    print(F.one_hot(X.T, len(vocab)).shape)

    # 验证一下我们手搓的循环神经网络是否输出正确的形状
    num_hidden = 512
    net = RNNModelScratch(len(vocab), num_hidden, d2l.try_gpu(), get_params, init_rnn_state, rnn)
    state = net.begin_state(X.shape[0], d2l.try_gpu())
    Y, new_state = net(X.to(d2l.try_gpu()), state)
    print()
    print(Y.shape)
    print(len(new_state))
    print(new_state[0].shape)

    # 不训练直接预测
    print("predict without training:\ntime traveller ...? ->")
    pred = predict_ch8("time traveller ", 10, net, vocab, d2l.try_gpu())  # 生成离谱的 预测结果
    print(pred)

    # 训练后再预测
    num_epochs, lr = 500, 1
    print("not random sample:")
    train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(), False)  # 不使用随机采样
    print("random sample:")
    train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(), True)  # 使用随机采样

output

tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0],
        [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0],
        [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0]])
torch.Size([5, 2, 28])

torch.Size([10, 28])
1
torch.Size([2, 512])
predict without training:
time traveller ...? ->
time traveller jckmckmckm
not random sample:
perplexity:  1.0546326766270984, 14819.88615243743 tokens / per second, on cpu
predict 'time traveller':
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby

random sample:
perplexity:  1.30568447689415, 14425.676215978849 tokens / per second, on cpu
predict 'time traveller':
time travellerit s against reason said filbywan a oft reaverathe
travellerit s against reason said filbywhat had in an at re

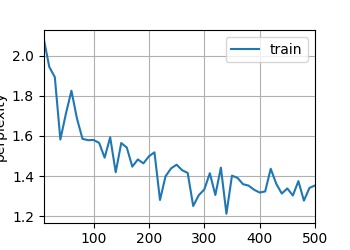
简洁实现的循环神经网络

此节中我们将使用深度学习框架中的高级API实现循环神经网络

code

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


# 为一个完整的循环神经网络模型定义一个RNNModule类
# 由于rnn_layer只包含隐藏的循环层，因此还需要创建一个单独的输出层
class RNNModel(nn.Module):
    """循环神经网络模型"""
    def __init__(self, rnn_layer, vocab_size, **kwargs):
        super(RNNModel, self).__init__(**kwargs)
        self.rnn = rnn_layer
        self.vocab_size = vocab_size
        self.num_hidden = self.rnn.hidden_size
        # 如果RNN是双向的，num_directions应该是 2，否则是 1
        if not self.rnn.bidirectional:
            self.num_directions = 1
            self.linear = nn.Linear(self.num_hidden, self.vocab_size)
        else:
            self.num_directions = 2
            self.linear = nn.Linear(self.num_hidden * 2, self.vocab_size)

    def forward(self, inputs, state):
        X = F.one_hot(inputs.T.long(), self.vocab_size)
        X = X.to(torch.float32)
        Y, state = self.rnn(X, state)
        # 全连接层首先将Y的形状改为(num_steps * batch_size, num_hidden)
        # 它的输出形状是(num_steps * batch_size, vocab_size)
        output = self.linear(Y.reshape((-1, Y.shape[-1])))
        return output, state

    def begin_state(self, device, batch_size=1):
        # LSTM: 长短期记忆网络：一种特殊的循环神经网络
        if not isinstance(self.rnn, nn.LSTM):
            # nn.GRU以张量为隐状态
            return torch.zeros((self.num_directions * self.rnn.num_layers,
                                batch_size, self.num_hidden), device=device)
        else:
            return (torch.zeros((self.num_directions * self.rnn.num_layers, batch_size, self.num_hidden),
                                device=device), torch.zeros((self.num_directions * self.rnn.num_layers,
                                                             batch_size, self.num_hidden), device=device))


if __name__ == "__main__":
    batch_size, num_steps = 32, 35
    train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
    num_hidden = 256
    # 定义模型
    rnn_layer = nn.RNN(len(vocab), num_hidden)
    # 初始化隐状态
    state = torch.zeros((1, batch_size, num_hidden))
    print(state.shape)

    X = torch.rand(size=(num_steps, batch_size, len(vocab)))
    Y, state_new = rnn_layer(X, state)  # rnn_layer就是之前的net

    # 训练与预测
    device = d2l.try_gpu()
    net = RNNModel(rnn_layer, vocab_size=len(vocab))
    net = net.to(device=device)
    predict = d2l.predict_ch8("time traveller", 10, net, vocab, device)
    print("predict of 'time traveller' without training:")
    print(predict)  # 这样得到的是一个胡扯的结果，因为没有训练
    print("start training:")
    num_epochs, lr = 500, 0.1
    d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device=device)
    d2l.plt.show()  # 可视化困惑度

output

torch.Size([1, 32, 256])
predict of 'time traveller' without training:
time travellerxvxcxvfxxx
start training:
perplexity 4.0, 50341.3 tokens/sec on cpu
time travelleryou ong thave dery ald har he hare ard an therimet
traveller and thas ed ane tore red ane trever tinntalle som

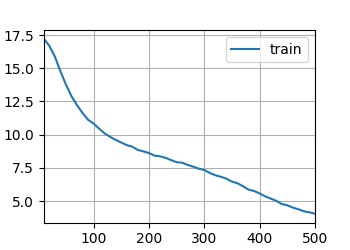
通过时间反向传播

本部分为纯理论介绍，详见9.7. Backpropagation Through Time — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

(•‿•)