贪心
贪心算法(含动态规划思想)
贪心算法是一种局部最优选择策略。它通过在每一步都选择当前状态下的最优解,试图最终得到全局最优解; 动态规划通过将问题分解为 子问题,逐步求解子问题的最优解,最终得到整个问题的最优解。它利用子问题的重叠性和最优子结构性质。
核心
贪心算法的核心思想是总在每一步抉择中挑选出当前最大/最小(即最值)对应的情况进行处理,从而达到最好/最坏的情况,满足贪心的目的
例题
通配符匹配
题目
给你一个输入字符串 (s) 和一个字符模式 (p) ,请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配:
'?'可以匹配任何单个字符。'*'可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
示例 1:
输入:s = "aa", p = "a" |
示例 2:
输入:s = "aa", p = "*" |
示例 3:
输入:s = "cb", p = "?a" |
提示:
0 <= s.length, p.length <= 2000s仅由小写英文字母组成p仅由小写英文字母、'?'或'*'组成
分析
暴力枚举的做法在此题是不可想象的,而暴力递归进行枚举贪心的做法也会因为复杂度过高而超时,因此必须结合动态规划的思想进行贪心优化。这个匹配规则类似于正则匹配,考虑用分治的思想进行动态规划:对于输入串s和匹配规则p,若对于串s的某个前缀s'可以和p的某个前缀p'匹配,则只要用相同的方法验证剩余的内容是否匹配即可(动态规划),对于不同的匹配规则采取不同的匹配策略,期望一次匹配掉所有可能的情况来保证后续判断的准确(贪心);匹配规则:
alpha: 匹配指定字符
?: 匹配单个任意字符
*: 匹配任意串,包括空串
为了使用动态规划,我们考虑建立一个由s长度和p长度共同组成的一个二维数组dp代表我们的迭代更新记录,下面尝试寻找并建立状态转移函数。想象一个棋盘,这个棋盘的行索引是输入串的每个字符,列索引是匹配规则的每个字符,不过最上面一行和最左边一列留空(为了留出起点且防止后续操作越界),我们在这个棋盘上移动,根据特定的匹配规则和输入字符,判断能不能从左上角(起点),走到右下角(终点),因此:
对于某个位置,如果可达,则记为true,反之为false,只能从记录为true的格子出发。初始时置最左上角即起点的格子为true,从这个位置开始移动。对于不同的通配符匹配规则,我们将其转化为对应的移动规则:
alpha: 如果当前读入一个字母通配符,则查看左边一列所有标记为true的格子,试者从这些格子往右下方走一步,如果右下方格子的行索引和读入的通配符一致
?: 同上查看规则,但在判断移动时不需要一致,只要左边一列的格子为true,就往右下方格子走一步
*: 因为’*'可以匹配所有读入字符,所以只要在左边一列从上往下找到第一个标记为true的格子,那么从这个格子开始先往右走一步(*可以匹配空串),之后从这个格子开始往下的每个格子都能走到(因为*可以匹配任意字符,有啥都能匹配,因此在自己这个位置来多少匹配多少),即左边一列找到第一个为true的行,此列中所有该行之下(含该行)的格子都标记为true。
最后查看最右下角的格子是否标记为true就知道是否匹配。
示例:
| 0 | a | * | ? | e | |
|---|---|---|---|---|---|
| 0 | start(true) | 留空(false) | 留空(false) | 留空(false) | 留空(false) |
| a | 留空(false) | true | true | ||
| b | 留空(false) | true | true | ||
| c | 留空(false) | true | true | ||
| d | 留空(false) | true | true | ||
| e | 留空(false) | true | true | true |
代码如下
|
加油站
题目
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] |
示例 2:
输入: gas = [2,3,4], cost = [3,4,3] |
提示:
gas.length == ncost.length == n1 <= n <= 1050 <= gas[i], cost[i] <= 104
分析
这题主要是找到贪心的策略,即某个符合特性的点。我们首先计算出每个加油站走到下一个站时获油和耗油间的差距,来得到未来一步净油量变化。这个净油量变化代表着走到下一加油站处油箱的实际变化。我们考虑一个“折线图”,从第一个加油站出发,计算净油量变化的前缀和代表一个点,每个点代表着每个加油站处油箱的油量,整张图表示油箱的变化。我们考虑一个最特殊的点:油箱油量最低的点——谷底(可能是负数);在这个谷底点之后的每个点都不会比这个谷底的油量还要低,即若从谷底之后的那个点出发,油箱中的油总是够用的,也就是题目所求的出发点。
“当你跌入谷底,之后的每一步都在爬升”
代码如下
class Solution { |
切蛋糕的最小开销
题目
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
horizontalCut的大小为m - 1,其中horizontalCut[i]表示沿着水平线i切蛋糕的开销。verticalCut的大小为n - 1,其中verticalCut[j]表示沿着垂直线j切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线
i切开蛋糕,开销为horizontalCut[i]。 - 沿着垂直线
j切开蛋糕,开销为verticalCut[j]。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
**输入:**m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
**输出:**13
解释:
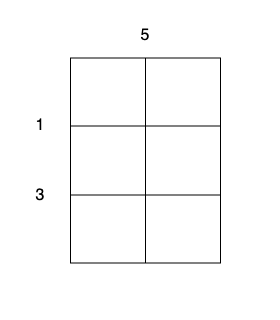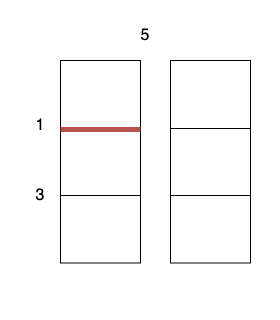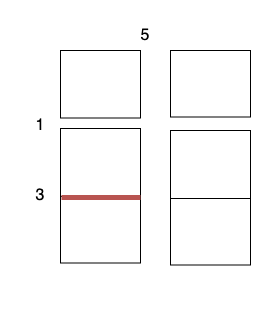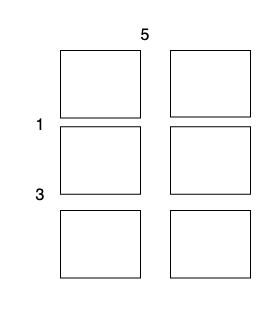
- 沿着垂直线 0 切开蛋糕,开销为 5 。
- 沿着水平线 0 切开
3 x 1的蛋糕块,开销为 1 。 - 沿着水平线 0 切开
3 x 1的蛋糕块,开销为 1 。 - 沿着水平线 1 切开
2 x 1的蛋糕块,开销为 3 。 - 沿着水平线 1 切开
2 x 1的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。
示例 2:
**输入:**m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
**输出:**15
解释:
- 沿着水平线 0 切开蛋糕,开销为 7 。
- 沿着垂直线 0 切开
1 x 2的蛋糕块,开销为 4 。 - 沿着垂直线 0 切开
1 x 2的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。
提示:
1 <= m, n <= 20horizontalCut.length == m - 1verticalCut.length == n - 11 <= horizontalCut[i], verticalCut[i] <= 103
分析
本题期望得到最小开销,可以采用贪心的思想。根据贪心的核心思想,我们在每一刀都要选择使得总开销最小的切法,那选择开销最大的还是最小的下刀呢?考虑到蛋糕每切一刀,产生的“碎片”就越多,比如我按行切了一刀,那就会多一行出来,之后所有没切的列都要多切一下。因为每个1 * 1蛋糕的连接处总是要下刀的,因此如果把开销大的留到后面切,需要处理的蛋糕碎片就会更多,也就是切更多刀来切断每个蛋糕的这一刀,这就会导致总开销增加,因此不能把开销大的留到后面(因为蛋糕在变成1 * 1前总会产生碎片的,总要有某些刀需要对很多碎片处理的,那把这些需要频繁切的刀留给开销小的,就可以使得开销降低),因此在每一刀选择时选择当前开销最大的,尽快切掉避免之后处理更多的碎片,并在切完后维护更新当前需要处理的行蛋糕数和列蛋糕数。按行切增加行,此刀开销由单次开销和列数决定;按列切增加列数,此刀开销由单次开销和行数决定。
代码如下
class Solution { |
